AVL树

特征

AVL树通过一系列的旋转操作来保持二叉树的平衡

实现

需要引入两个概念：

高度，即height变量
节点平衡因子(balance factor),定义为左子树的高度减去右子树的高度，规定空节点的平衡因子为0，AVL树中任何节点的平衡因子满足 $-1\le f \le 1$

/* AVL 树节点类 */
struct TreeNode {
    int val{};          // 节点值
    int height = 0;     // 节点高度
    TreeNode *left{};   // 左子节点
    TreeNode *right{};  // 右子节点
    TreeNode() = default;
    explicit TreeNode(int x) : val(x){}
};

/* 获取节点高度 */
int height(TreeNode *node) {
    // 空节点高度为 -1 ，叶节点高度为 0
    return node == nullptr ? -1 : node->height;
}

/* 更新节点高度 */
void updateHeight(TreeNode *node) {
    // 节点高度等于最高子树高度 + 1
    node->height = max(height(node->left), height(node->right)) + 1;
}

/* 获取平衡因子 */
int balanceFactor(TreeNode *node) {
    // 空节点平衡因子为 0
    if (node == nullptr)
        return 0;
    // 节点平衡因子 = 左子树高度 - 右子树高度
    return height(node->left) - height(node->right);
}

AVL树的旋转

当一个阶段的平衡因子绝对值>1时（自下往上），需要调整，使节点平衡分四种情况：

==右旋== 右旋1
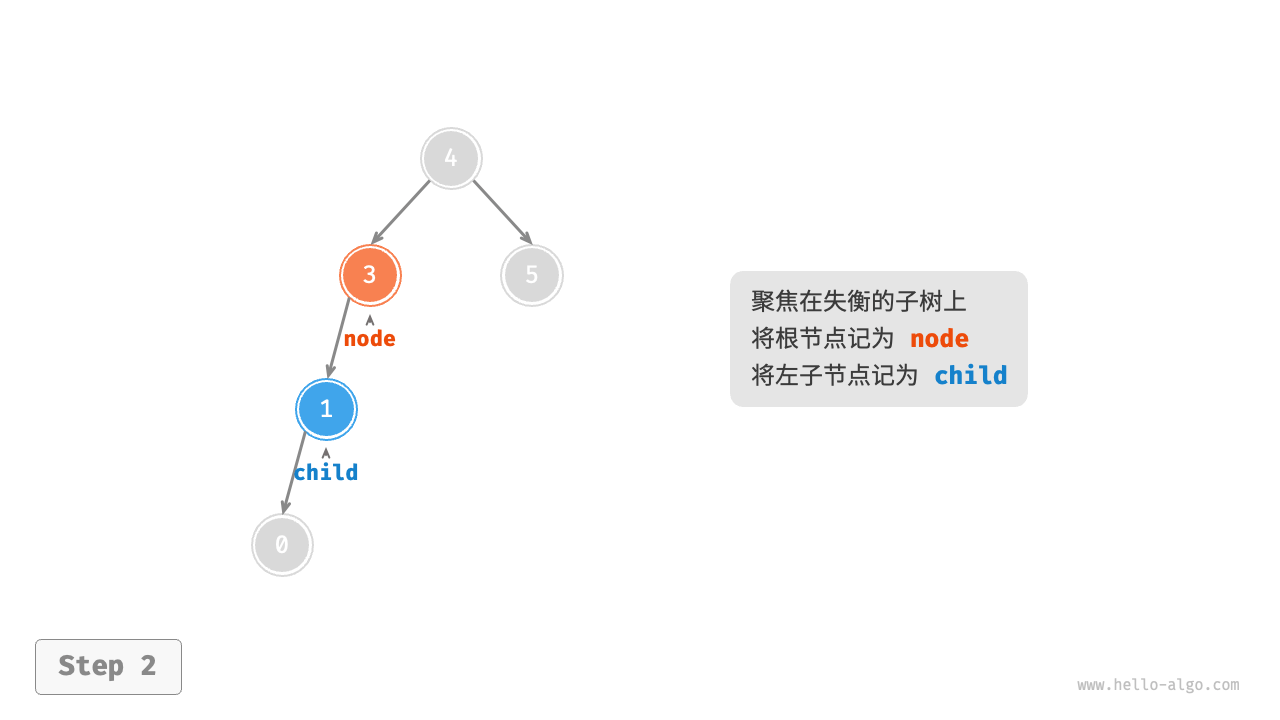
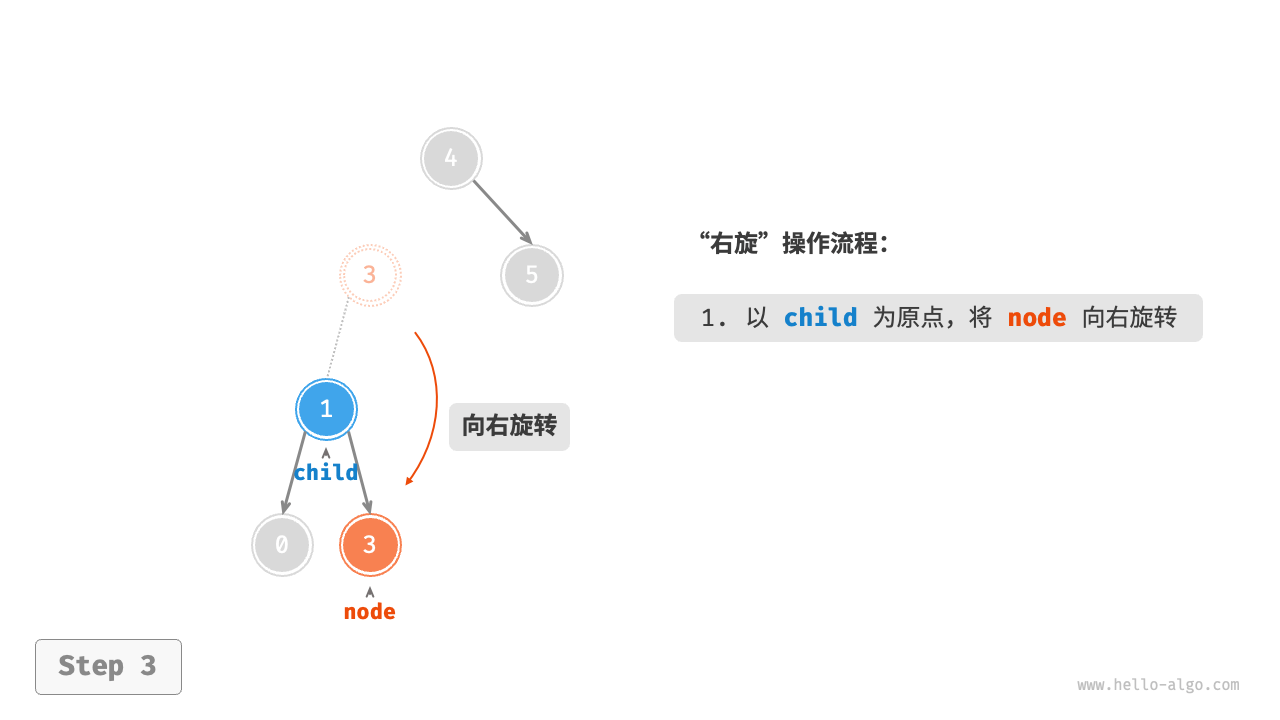
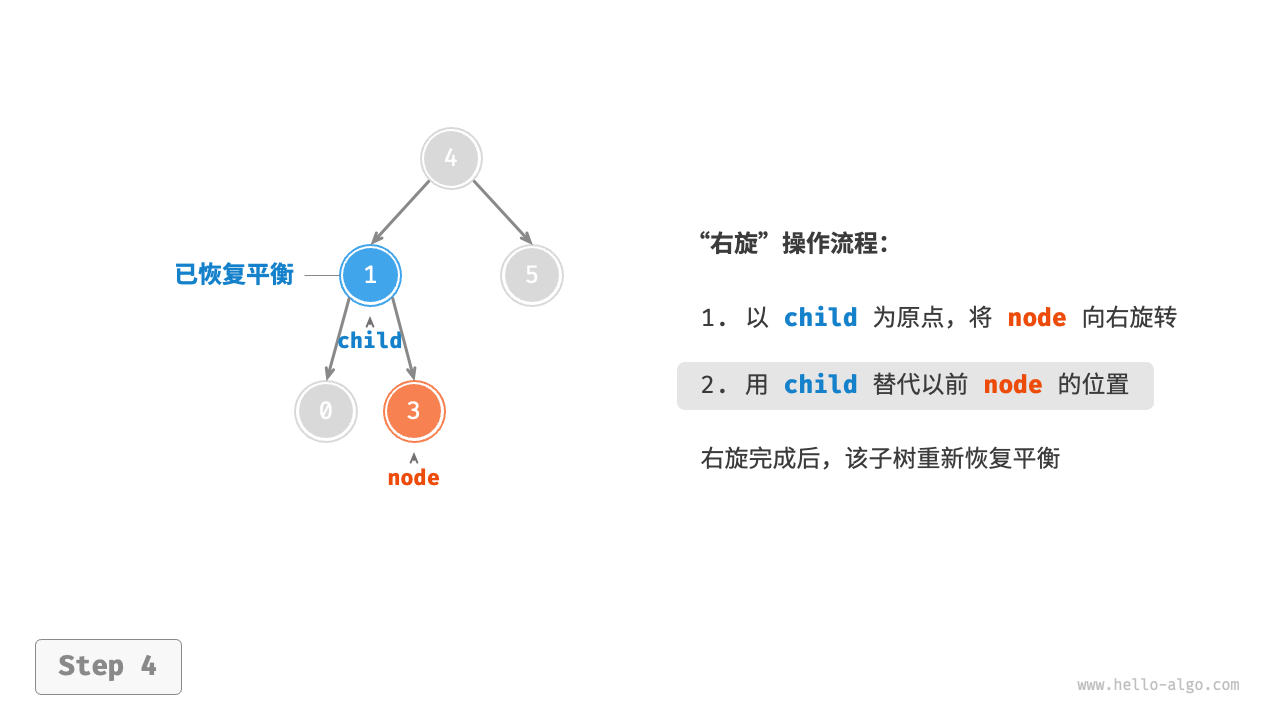右旋2 右旋3 当节点child有右子节点时，需要在右旋中加一步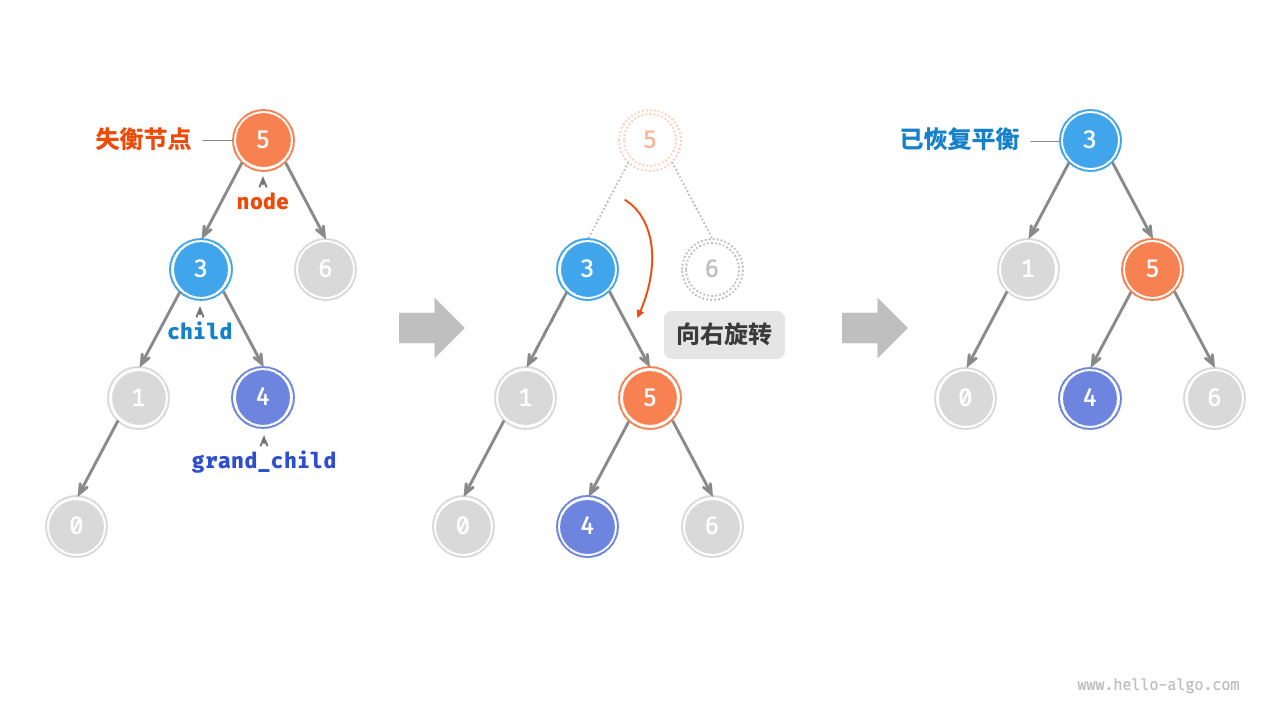右旋4 实现方法：

/* 右旋操作 */
TreeNode *rightRotate(TreeNode *node) {
    TreeNode *child = node->left;
    TreeNode *grandChild = child->right;
    // 以 child 为原点，将 node 向右旋转
    child->right = node;
    node->left = grandChild;
    // 更新节点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根节点
    return child;
}