树的算法部分
树的算法部分
广度优先探索BFS
/*>>>>>>>>>>>>>>>>BFS<<<<<<<<<<<<<<<<<<<<<<<<*/
vector<int> levelOrder(TreeNode * root){
queue<TreeNode *>q;
q.push(root);
vector<int> vec;
while(!q.empty()){
TreeNode * node=q.front();
q.pop();
vec.push_back(node->val);
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
return vec;
}
原理如下:
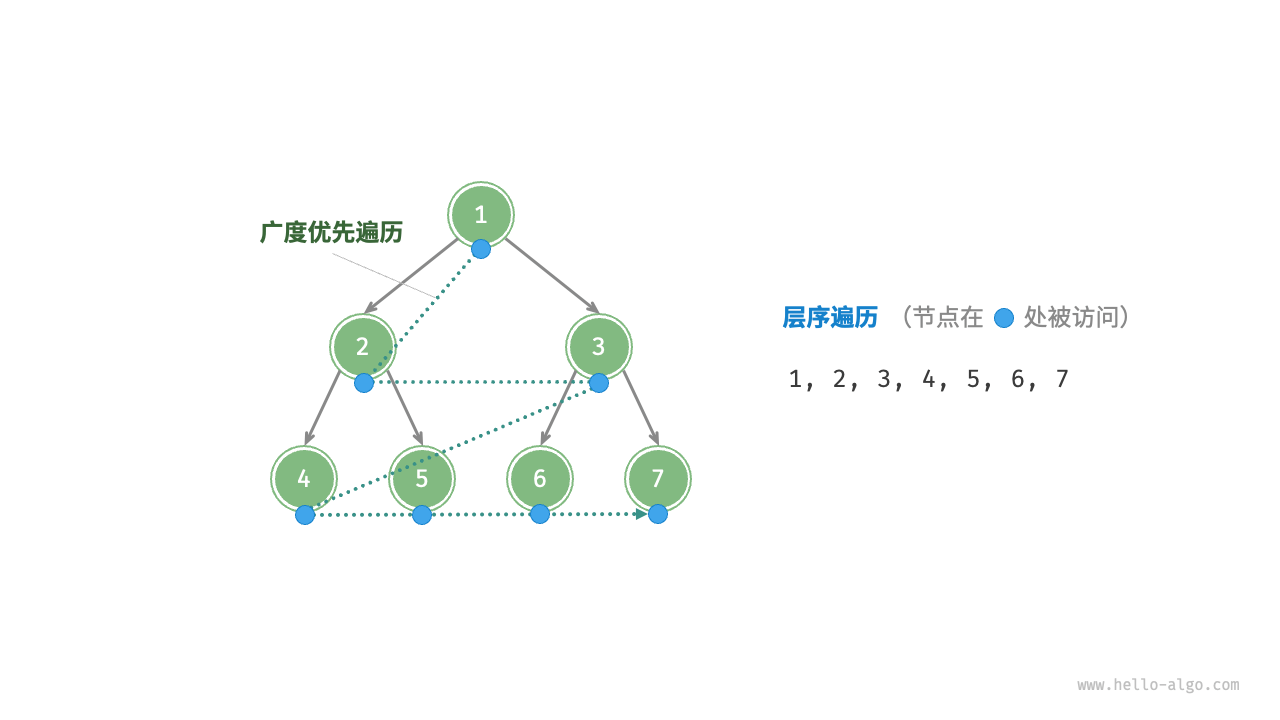
深度优先搜索DFS
/*>>>>>>>>>>>>>>>>DFS<<<<<<<<<<<<<<<<<<<<<<<<<<<<<*/
vector<int> vec;
/*前序遍历*/
void preOrder(TreeNode * root){
if(root==nullptr)
return;
//根节点->左子树->右子树
vec.push_back(root->val);
preOrder(root->left);
preOrder(root->right);
}
/*中序遍历*/
void inOrder(TreeNode * root){
if(root==nullptr)
return;
//左子树->根节点->右子树
inOrder(root->left);
vec.push_back(root->val);
inOrder(root->right);
}
/*后序遍历*/
void postOrder(TreeNode * root){
if(root==nullptr)
return;
//左子树->右子树->根节点
postOrder(root->left);
postOrder(root->right);
vec.push_back(root->val);
}
树的效率分析
如果二叉树能够达到平衡,效率为,如果二叉树失衡而退化成链表,则效率为
改进方法: AVL树